We had a discussion the other day at work about Arthur Eddington, of solar eclipse fame. It started with a tweet from @landetannien about proofs in science.

The point of the tweet being that she’s frustrated with people insisting that science needs to prove things. That reminded me of a quotation by Eddington from his Gifford lectures, collected by H. G. Callaway in the book The Nature of the Physical World:

We cannot pretend to offer proofs. Proof is an idol before whom the pure mathematician tortures himself. In physics we are generally content to sacrifice before the lesser shrine of Plausibility.

Arthur S. Eddington, The Nature of the Physical World: Gifford Lectures of 1927

I like this quotation, but reading about Eddington on Wikipedia I was delighted to find out that there is such a thing as an Eddington number for bicycling. I works similarly to the Hirsch-index so important in academia nowadays. An Eddington number, or E-number, of 50 means that you have bicycled at least 50 miles 50 times during your life (or other relevant period). That means that increasing the E-number can be quite hard, since that can require quite a number of trips.

I’m a bit of obsessive when it comes to collecting statistics about things. I have an excel sheet with the distance I cycled every day since 2008, so with that data at hand I decided to calculate my own E-number. Wikipedia says that Eddingtons E-number was 84! That’s really good! I like cycling and I cycle to work as often as I can, but I rarely go for any longer trips so my E-number will be much lower.

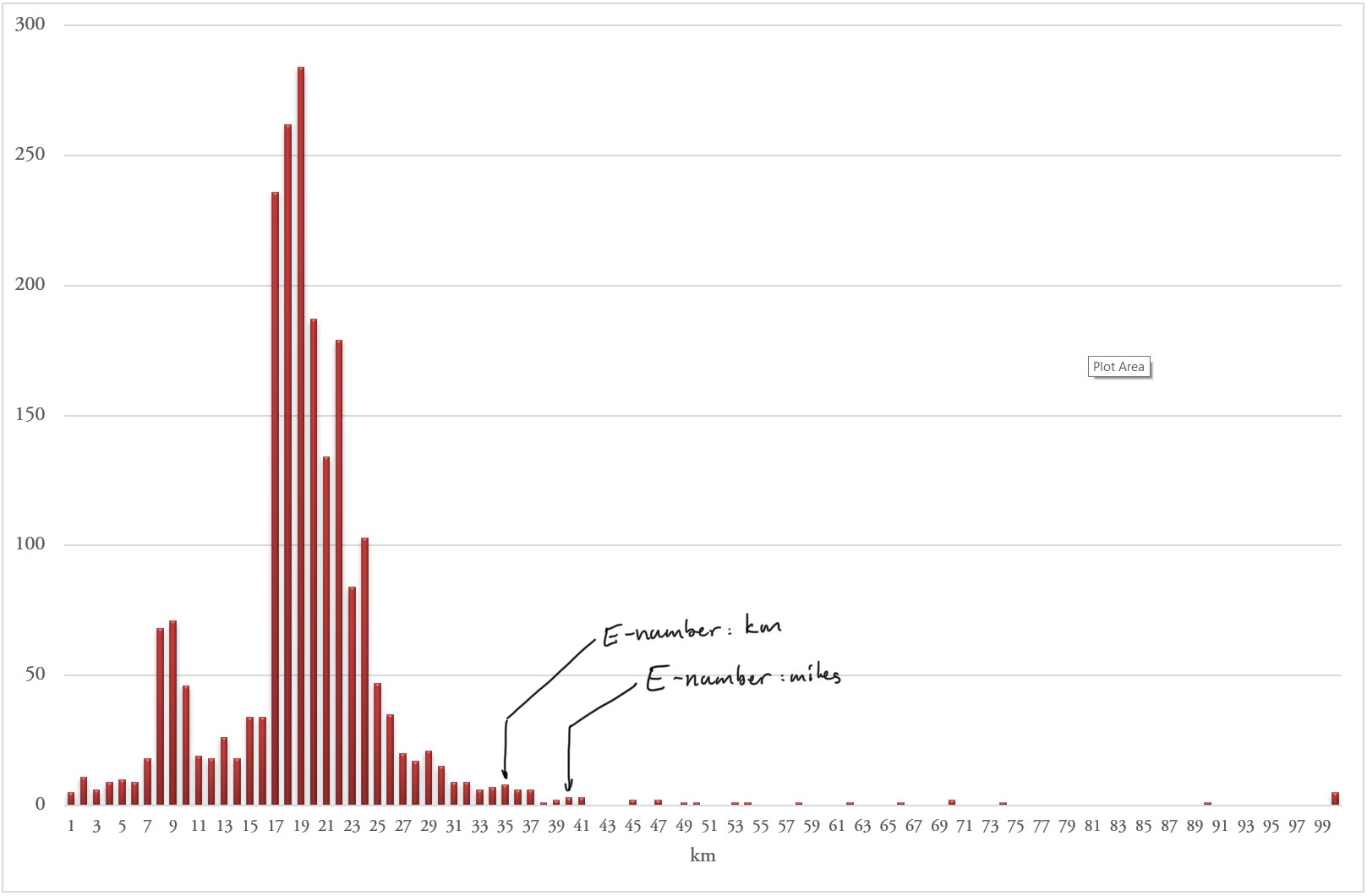
The histogram of my cycling shows two distinct peaks. The highest one is my daily commute. From that one could easily guess that my distance to and from works sums up to about 20 km. But that’s not actually the case. In fact I have about 17.5 km to work and back. That the peak is at 19 is that I used to live slightly further from work and that I sometimes take detours on the way. The second peak represents the times that I took the bike to work one day and home the next. But it’s also clear that I’m not often going on longer bike rides. I used to do that much more when I was younger and didn’t have a child, but that was before I started writing down my daily kilometre count.

Using the data I have, my E-number is 25! That is I have cycled further that 25 miles on at least 25 days¹. 25 miles is about 40 km, but I have not cycled 40 km on more than 40 days. Instead, my E_km-number is 35! The data also shows me that if I want to increase my E-number to 26 I will need to make another 5 rides above 26 miles². To increase the E_km-number I need only a single ride above 36 km.

So there it is. Eddington, apart from being a terrific physicist, was a heck of a bicyclist. I have some catching up to do. What is your E-number?

1. If fact I have done this exactly 25 times
2. That sounds a lot more doable than running 5 marathons!